앞서 길찾기 알고리즘 관련해서 2개의 알고리즘(Dijkstra, BidirectionalDijkstra)에 대해 살펴봤다. 컴퓨터를 활용하여 길을 찾아가는 알고리즘의 목적은 크게 최적의 경로를 최대한 빨리 찾아내는 것이라 할 수 있다. 이론적으로 이들 알고리즘은 최적의 경로를 찾아주는 것을 보장하지만 최대한 빨리 찾는 것에는 한계를 드러내고 있다. 앞에서 설명한 BidirectionalDijkstra 알고리즘도 이런 맥락에서 탐색속도를 개선하기 위한 하나의 방법으로 볼 수 있다. 이처럼 Dijkstra Algorithm의 탐색 속도는 탐색공간 크기에 종속적일 수 밖에 없으며 나아가 길찾기가 한 국가를 넘어 글로벌 규모로 확대해 나간다면 탐색 속도는 서비스 경쟁력을 유지에 중요한 걸림돌이 될 수밖에 없다.

최근들어 Dijkstra Algorithm과 같이 전통적인 길찾기 알고리즘에만 의존하는 것이 아니라 교통공학적인 요소를 길찾기 알고리즘에 접목시킴으로써 탐색속도를 획기적으로 개선하는 시도들이 이어지고 있다. 그 중 가장 눈에 띠는 방법으로 이미 글로벌 또는 국내 내비 업체에서 도입하고 있는 것이 Contraction Hierarchy이다. 이 글에서는 Contraction Hierarchy가 어떤 개념을 적용하고 있으며 이렇게 함으로써 어느정도의 속도 향상을 얻을 수 있는지에 대해 얘기해 보고자 한다.

경로탐색의 재해석

앞서 봤듯이 Dijkstra Algorithm은 하나의 출발지에서부터 도달 가능한 모든 노드들에 대해 최단경로를 찾아낸다(SSSP: Single-Source Shortest Path. 하지만 현실적으로 봤을 때 우리는 가고자 하는 목적지까지의 최단 경로가 중요하지 그 외의 경로에 대해서는 관심이 없다. 즉, 출발지와 목적지 사이의 최단경로가 관심의 대상이지 하나의 출발지에서 도달 가능한 모든 지점들간의 최적경로는 무의미히다는 것이다.

이 경우 Dijkstra Algorithm이 탐색과정에서 목적지를 만날 경우 탐색을 종료해버리면 더이상 불필요한 탐색을 진행하지 않을 수 있다. 이런 생각까지 이어졌다면 Dijkstra Algorithm을 현실 도로에 적용할 경우 어느정도 효율적일까라는 질문을 던질 수 있다. 그냥 처음 드는 생각은 단순 무식한 방법(brute-force)이이라고 느낄 수 있다.

앞에서 설명한 Dijkstra Algorithm에서 봤듯이 언뜻 드는 생각은 목적지 방향과 관련이 없는(역방향) 노드들을 굳이 찾는데 시간을 소요할 필요가 있을까? 또는 목적지를 찾아가는데 고속도로를 이용하는 것이 합리적이라면 굳이 뒷골목 도로까지 찾아 갈 필요가 있나? 라는 생각을 하는 것이 당연하다.

아래와 같이 녹색으로 표시된 출발지와 오렌지 색으로 표시된 목적지를 가진 그래프를 생각해보자.

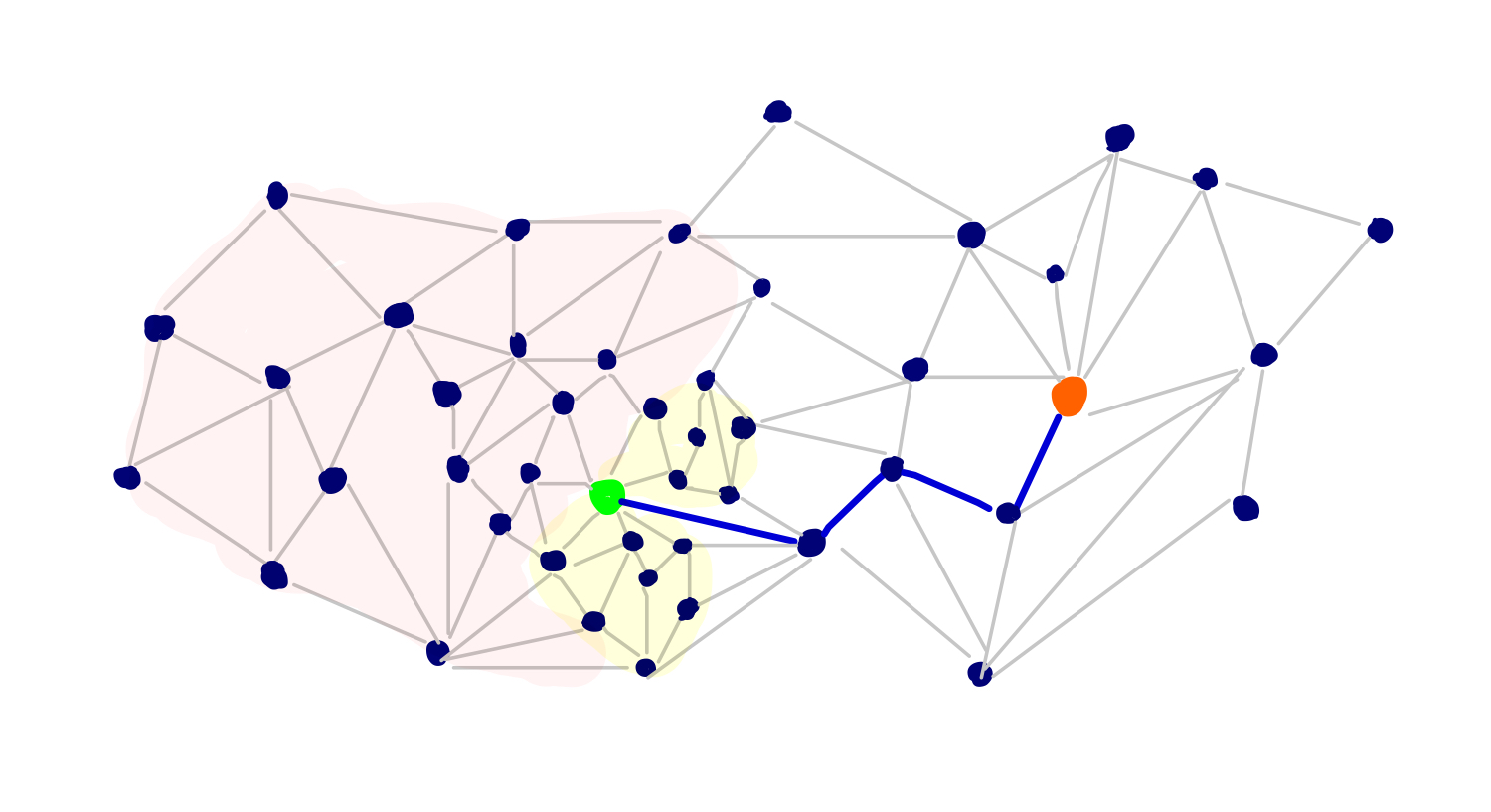
이 그래프를 대상으로 Dijkstra Algorithm을 적용한다고 했을 때 목적지 위치를 감안하면 붉은 색 영역은 굳이 탐색하지 않아도 되지 않을까라고 생각할 수 있다. 또한 뒷골목과 같은 노란색의 영역도 굳이 탐색할 필요가 없으므로 탐색에서 제외시키고 싶을 것이다. 이렇게 보면 목적지로 향하는 그래프상에서도 dist() 거리 점수가 낮은 노드들이 많이 있을 수 있는데 이런 노드들은 최종 생성되는 최단경로와 관련성은 그리 높지는 않을 수 있다.

만약 두 노드사이의 지름길을 이미 알고 있는 상태라라면 굳이 탐색이 필요없는 영역들은 쉽게 찾아낼 수 있을 것이다. 그러나 도로의 중요도 측면에서 어떤 도로(링크)가 어떤 도로보다 더 중요한지 알아내는 것은 고속의 Algorithm 제작에서 쉽지 않은 영역이다.

증강된 그래프 모델(Augmented Graph)의 필요성

도로 모델링에 사용되는 방향성 그래프(Directed Graph)는 앞에서 설명한 개념들을 반영하지 않고 있다. Dijkstra Algorithm은 이론적 증명을 통해 최단경로를 찾아주긴 하지만 대부분의 경우 필요 이상으로 그래프의 많은 영역을 탐색한다. 이런 고민들이 쌓여 더 효율적인 경로탐색 알고리즘을 설계하는 계기를 제공한다.

도로의 중요도, 위치, 타입(레벨 등)등의 정보를 어떻게 그래프에 반영하면 결과적으로 탐색범위(Search Space)가 줄어들도록 만들 수 있을까?

바꿔말하면 그래프에서 적은 수의 노드와 링크를 방문하고도 검증 가능한 최단경로를 찾을 수 있다면 출발지와 목적지 사이의 경로탐색 속도는 극적으로 빨라질 것이다.

어느정도의 속도개선이 가능할까?

Contraction Hierarchy Algorithm을 적용하면 어느정도의 속도개선이 가능한지 맛보기로 벤치마킹 결과를 한 번 보자.

아래의 표는 서로 다른 알고리즘을 활용하여 서부유럽의 도로네트워크를 대상으로 경로탐색을 한 결과이다. 이 표는 알고리즘이 탐색한 정점(vertices, 노드) 수와 탐색시간을 보여준다.

Algorithm	# of Scanned Vertices	Query Time(microseconds)
Dijkstra	9326696	2195080 (~ 2 seconds)
Contraction Hierarchies	280	110

우리가 알고 있는 Dijkstra Algorithm의 특성을 감안하면 앞에서도 얘기했듯이 속도를 개선하기 위해서는 탐색공간(Search Space)을 줄일 수 있는 정보들을 활용하여 그래프를 개선하는 방법밖에 없다.

그럼 이제 속도개선에 활용되는 몇가지 기술범주를 알아본 다음 Contraction Hierarchy의 기반을 다져 보도록 하자.

속도개선 방법

속도개선 기술은 크게 2가지 형태로 나눌 수 있다.

• 전처리(Preprocessing)
  추가적인 정보를 이용하여 그래프를 변형한다.
• 알고리즘 Query 수정(Modifications to Dijkstra Query)
  탐색과정에서 불필요한 노드들을 배제

Contraction Hierarchy와 같은 빠른 경로탐색 알고리즘은 전처리 과정에서 생성된 정보들을 활용하여 탐색 알고리즘의 Query동작을 수정하는 형태로 접근한다.

전처리(Preprocessing)와 Query의 TradeOff

최근들어 여러 자료에서 속도개선 기법을 심도있게 다루고 있지만 여기서는 중요한 개념 즉, 전처리 시간과 Query 시간의 tradeoff에 대해 다루고자 한다. 앞에서도 얘기했지만 경로탐색의 최우선 목표는 가장 빠른 탐색시간을 위해 적절한 방법으로 탐색공간을 줄이는 것이다.

한 극단적인 방법은 전처리 과정을 이용하여 그래프의 모든 노드들간 최단거리를 사전에 계산한 다음 테이블 형태로 저장해 놓으면 된다. 이렇게 하면 최단거리 탐색 과정이 필요없으며 최악의 경우에도 가장 빠른 성능을 얻을 수 있다. 물론 전처리 단계에 소요되는 시간은 6일 이상이 결릴 수 있다.

가능한 빠른 전처리 시간을 원한다면 Dijkstra Algorithm을 정공법으로 적용하면 된다. 이 경우 모두가 예상하듯 전처리에 소요되는 시간은 없다. 따라서 경로탐색 알고리즘은 전처리 시간과 Query 시간 사이에서 적절한 균형점을 찾아야 함을 알 수 있다.

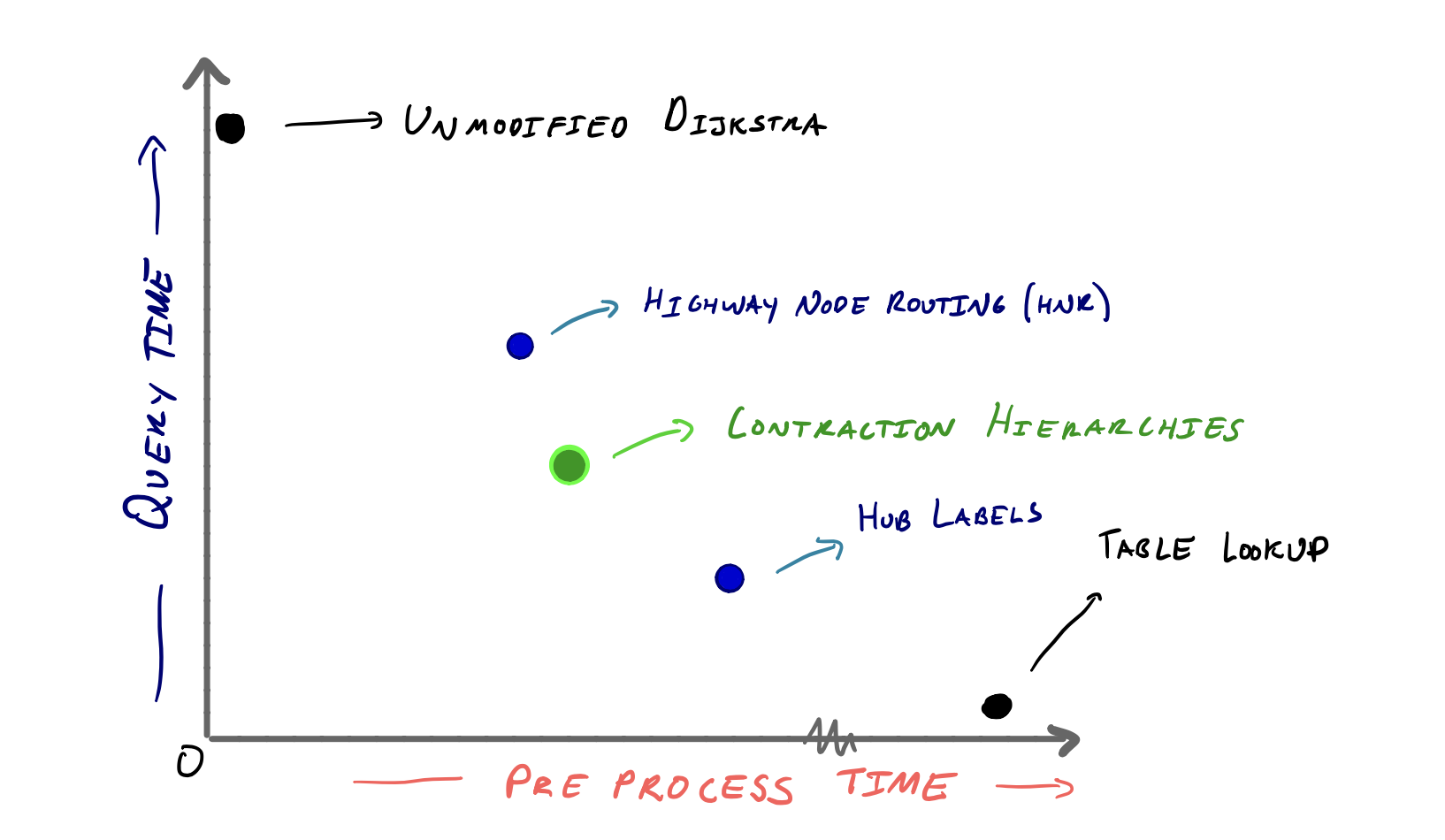
위 그래프는 다양한 알고리즘을 대상으로 전처리 시간과 Query시간의 상간관계를 보여준다. Contraction Hierarchy Algorithm이 TradeOff관점에서 어디쯤 위치하는지를 보여주는 정도로 생각하면 된다. 파란 점으로 표시된 알고리즘은 Contraction Hierarchy에 영향을 주거나 영향을 받은 알고리즘으로 보면 된다. 튜닝을 제대로 한 Contraction Hierarchy는 전처리에 소요되는 시간이 약 5~10분 정도라고 한다.

이런 TradeOff가 있다는 것을 감안할 때 그래프 개선을 위해서는 양질의 정보가 필요하고 또한 효율적인 방법으로 처리해야 한다. 이런 측면에서 도로 네트워크의 계층적 특성을 고려해 보는 것은 좋은 출발점이 될 수 있다.

The Hierarchical Nature of Road Networks

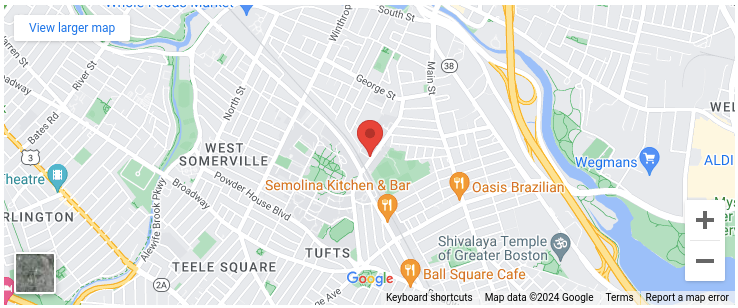
아래의 구글맵을 보면 특정 지점(Halligan Hall, the main CS building at Tufts)에 마커가 찍혀있다. 이 지도 영역을 한 단계 축소해 보면 그 다음 지도와 같이 된다.

이 상태에서 아래 지도와 같이 한번 더 축소하면 가늘고 하얀색이었던 도로가 좀 두께가 있는 하얀색의 도로와 일부 노란색의 도로가 보이기 시작할 겻이다.

여기서 몇 번 더 축소를 하게 되면 초기 하얀색이있던 도로는 사라지고 여기서 더 축소해버리면 두꺼웠던 하얀색 도로도 사라질 것이다. 이렇게 계속해서 NewYork이 보일 정도로 축소하면 아래 지도와 같이 이제 두껍고 노란색의 고속도로만 보일 것이다.

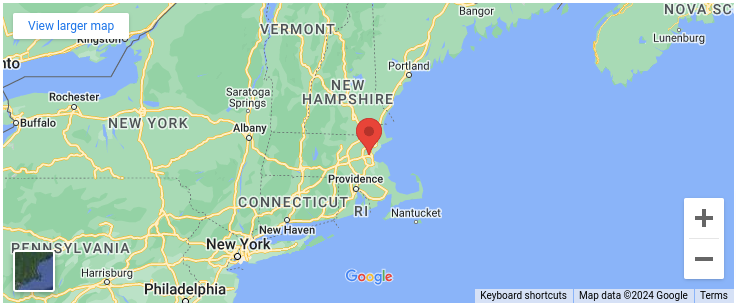
위의 설명이 의미하는 바는 도로 네트워크가 매우 계층적으로 구성되었음을 강조하는 것이다. 구글맵 뿐만 아니라 다른 지도들도 확대/축소를해 보면 이런 개념을 잘 적용하고 있다.

가까운 거리의 출발지와 목적지 사이의 최단경로일 경우 두껍고 하얀색의 도로외에 출발지/목적지 주변의 얇으면서 하얀색의 도로에만 관심을 가질 것이다. 위 지도의 출발지에서 New York까지의 최단경로를 찾는다면 대부분 노란색의 도로에 더 관심을 가질 것이다. 사실 출발지에서 Philadelphia까지 가는 최단 경로는 대부분 이들 노란색의 도로를 이용할 것이고 이들 도로의 많은 부분은 New York까지 가는 길과 겹칠 것이다.

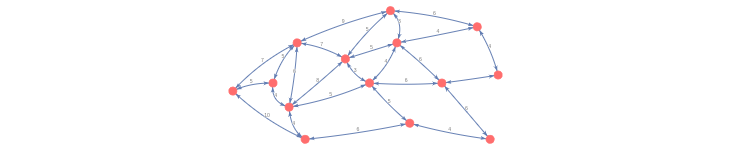
축소한 지도에서는 확대된 지도보다 더 적은 노드와 Edge(Link)를 가지지만 시각화해서 보면 최단경로상에서 실질적으로 중요한 노드와 Edge의 수를 파악하는데 도움을 준다. 다시말해, 초기에는 도로네트워크를 아래 그림과 같이 모델링 했었지만

앞에서 구글맵으로 설명했듯이 그래프에 개념적으로 포함시키고 싶은 정보는 아래와 같다.

계층적 정보를 이용하면 무엇을 할 수 있을까?

위 구글맵의 예로 돌아가 출발지에서 New York까지의 최단경로를 생각해보자. 맢서 말했듯이 대부분의 노란색 도로에 관심을 가질 것이며 이는 일반적으로 주행산 거리 대비 소요시간이 짧을 것이므로 원거리 여행은 고속도로를 이용할 것이라고 이해할 수 있다.

또한 고속도로에 들어서면 목적지 근처에 도달할 때까지 되도록이면 고속도로를 벗어나러고 하지 않을 것이다. 다시말해 원거리의 최단경로를 주행하면서 노란색의 도로와 하얀색의 도로를 자주 번갈아 가면서 이용하지는 않을 것이라고 예상할 수 있다.

개념적 모델

이제 모든 도로 Edge(링크)들에 대해 중요도(level of importance)를 기준으로 분류해보는 것을 생각해 볼 수 있다. 예를 들어 고속도로의 중요도는 이면도로보다 더 높다고 생각할 수 있다. 그러면 출발지와 목적지 사이에 Dijkstra Algorithm을 실행할 때 이전 단계에서 탐색했던 Edge보다 중요도가 높은 Edge에 연결된 노드를 대상으로만 Heuristic하게 탐색해 나갈 수 있다.

이렇게 함으로써 탐색과정에서 많은 수의 노드를 제외시킬 수 있으며 효과적으로 탐색공간을 줄일 수 있다.

아직까지 Edge들을 분류하는 효율적인 방법에 대해 설명하지 않았으므로 여기서는 이런 계층적 개념이 Contraction Hierarchy에서 사용되는 개념과 동일하다는 정도로만 알아두자.

Contraction Hierarchy의 이해

양방향 경로 탐색(별개의 주제임)과 도로의 계층적 특성은 훨씬 빠른 알고리즘 제작에 기반이 되는 유용한 구성요소로 작용한다. 이 두 구성요소를 접목함으로써 할 수 있는 것으로는

(1) 전처리(Preprocess): 일종의 중요도 개념에 따른 Node와 Edge 분류

(2) 탐색(Query): 중요도가 높은 Edge방향으로만 양방향 탐색 진행

이는 중요도가 낮아 최단경로상에 포함되지 않을 것으로 예상되는 링크들을 그래프에서 제외시켜 나감으로써 결국 전체 Edge(링크)의 수를 줄인다는 것에 기반을 두고있다. 계층적 레벨로 이루어진 도로가 그래프상에 최종 결과로 남게 될 것이며 이는 양방향 탐색을 가능하게 한다. 그러나, Node를 줄세우기 위해 Edge Reduction방법을 이용할 경우 많은 비용이 수반된다.

대신, Contraction Hierarchy 알고리즘은 Node Contraction을 이용하여 계층적 구조를 만든다. 여기서 모든 개별 노드는 각자 고유한 중요도에 속하게 된다.(다시 말해 중요도에 따른 노드의 정렬이라 할 수 있음)

Contraction과정을 거치면 일련의 지름길 Edge(shortcut edge)가 그래프에 추가되고 유지된다. 이후 양방향 탐색과정에서 중요도가 낮은 단계에서부터 높은 단계의 Node로 이어지는 Edge만을 대상으로 탐색을 하며 이들 Edge들 중에는 지름길 Edge도 포함될 수도 있다.

결과적으로 CH 알고리즘에 대한 개괄적인 설명은 아래와 같이 기술할 수 있다. 그리고 이후 내용에서 핵심 요소에 대한 상세한 설명을 이어나가도록 하겠다.

거시적 관점의 CH Algorithm:

Preprocess:

• 중요도 레벨에 따른 Node 줄세우기
• 가장 덜 중요한 노드에서 가장 중요한 노드 순으로 Contraction 수행

Query:

• 양방향 Dijkstra 탐색을 적용하며 이때 중요도가 높은 노드로 이어지는 Edge만을 탐색 대상으로 함

Node Contraction

하나의 Node를 축소(Contract)할 때 먼저 대상이 되는 Node를 그래프에서 제외시킨다. 만약 Contraction 전에 제외된 Node가 이웃하는 두 노드 사이의 최단경로상에 위치하고 있다면 이들 두 이웃 Node사이에 지름길(shortcut) Edge를 추가한다. 이때 최단경로상의 거리(최단거리)는 지름길 Edge에 유지되도록 한다.

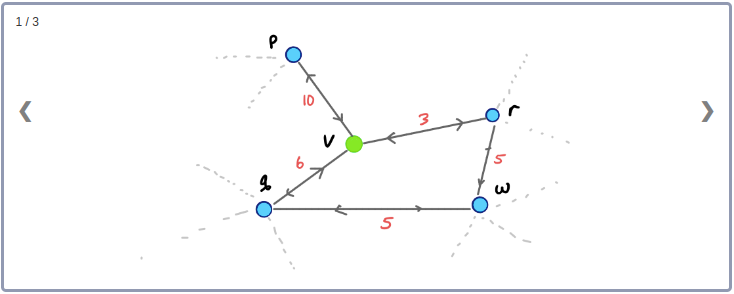
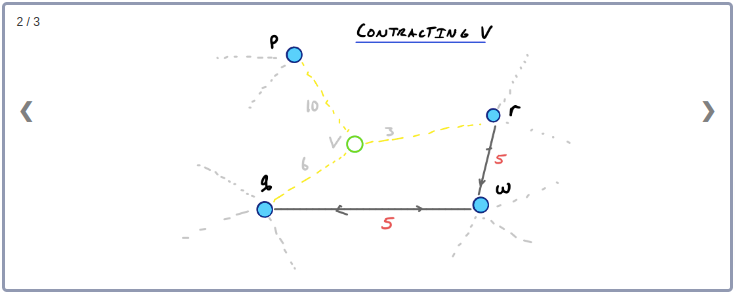
간단한 예를 들어보자. 아래 그림에서 Node v를 제외시키면 2개의 Edge를 제외하고 v, p, q, r 사이의 Edge는 모두 사라지게 된다.

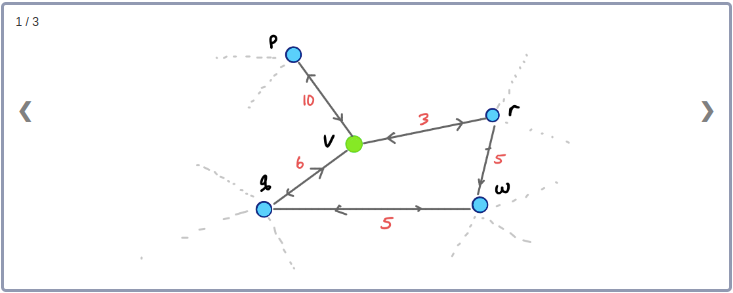
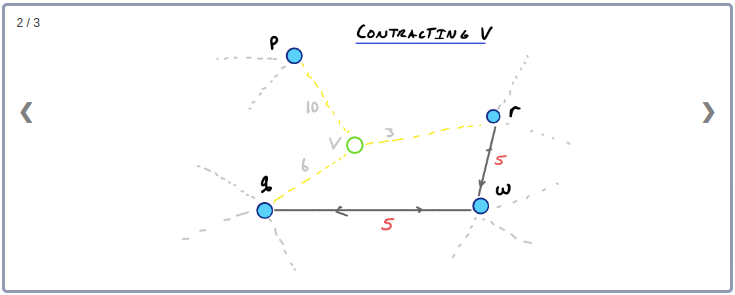
먼저 Node v와 인접하고 있는 Edge들을 그래프에서 제외시킨다. 그런 다음 v와 이웃하고 있는 두 노드 사이의 최단경로들 중 v를 지나가는 최단경로가 존재하는지 확인한다. 이 예제에서는, p와 r, q와 r, p와 q의 최단경로는 모두 v를 지나간다. 따라서 지름길 Edge pr, qr, pq를 추가한다. 이때 지름길 Edge의 weight는 contract된 링크의 weight를 더한 값(최단거리)으로 설정한다.

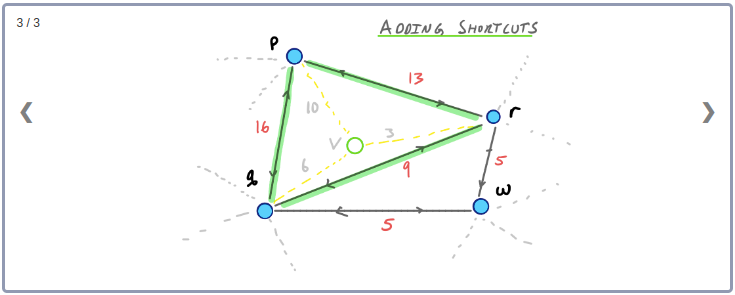
노드 v와 인접하고 있는 Edge들을 제외시켰을 때 q에서 r로 이어지는 경로가 비록 존재하더라도 q와 r사이의 최단경로는 아니므로 지름길 Edge qr은 필요한 상황이 된다.

일반적 정의(Formal Definition)

Node v로 인입하는 모든 Edge의 시작(from) 정점(vertices, node)들로 구성된 집합을 U라 하고 Node v에서 뻗어나가는 Edge에 대응하는 끝(to) 정점들로 구성된 집합을 W라고 할 때

U집합의 한 원소인 u와 W집합의 한 원소인 w인 각 정점들의 쌍(v, w)에 대해

만약 경로 <uvw>가 u에서 w로 가는 유일한 최단경로일 경우 지름길 Edge uw를 그래프에 추가한다. 이때 지름길 Edge의 weight는 w(u, v) + w(v, w)로 한다.

그런 다음 노드 v에 인접한 모든 Edge들을 그래프에서 제외시킨다. 이렇게 하면 Node v에 대한 Contraction이 종료된다.

모든 노드들을 상대로한 Contraction

앞에서 설명한 Node Contraction을 감안하면 CH알고리즘은 Node간의 특정 순서를 기반으로 각 Node들을 Contraction하고 있음을 시사한다.

지금은 이 Node들 간의 순서가 이미 정해져 있다고 가정하자. 곧 알게 되겠지만 좋은 Node Ordering(순서) 부여는 고속 CH알고리즘에서 가장 핵심적인 부분를 차지한다. 그렇지만 순서가 임의로 부여된다 하더라도 양방향 탐색은 정상적으로 동작한다는 것을 증명해 볼 것이다.

순서에 따른 Node Contraction을 설명하기 위해 임의의 중요도 레벨에 따라 Node들을 사전에 줄세워 놨다고 생각해보자.

그런 다음 [1, n]으로 이어지는 각 처리 단계 i 에서 정점(Vertex, Node) v_i 와 인접하고 있는 모든 Edge들을 그래프에서 제외시킴으로써 정점 v_i 를 contract 시킨다.

i + 1번째 단계의 그래프에는 n – i 개수의 노드만 남게 된다. 하지만 그래프에는 이 전단계에서 추가된 지름길 Edge들도 같이 포함되게 된다. 지름길 Edge와 인접한 Node가 Contract될 경우에도 이 지름길 Edge를 동일한 방법으로 그래프에서 제외(contract)시켜 나간다.

덧댄 그래프(The Overlay Graph)

노드 v_n 까지 Contract하고 나면 초기에 있었던 모든 Node와 Edge 그리고 Contraction 과정에서 추가된 모든 지름길 Edge들을 포함하는 그래프인 G*를 생각할 수 있다. 이 그래프 G* 를 양방향 Dijkstra 탐색에 활용한다.

Example

모든 Node들의 Contraction 과정을 시각화하기 위해 아래와 같이 임의의 Node순서로 구성된 그래프를 생각해보자.

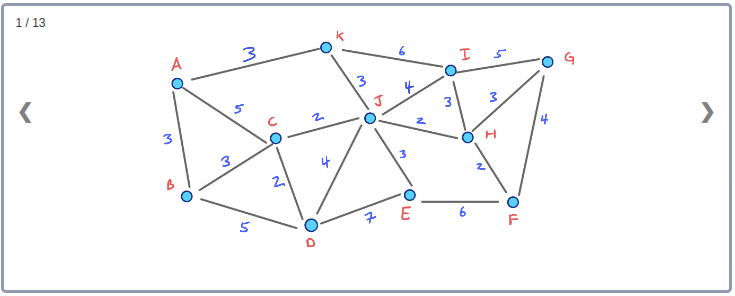
이 그래프의 Contraction과정을 순서대로 표현하면 아래와 같다.

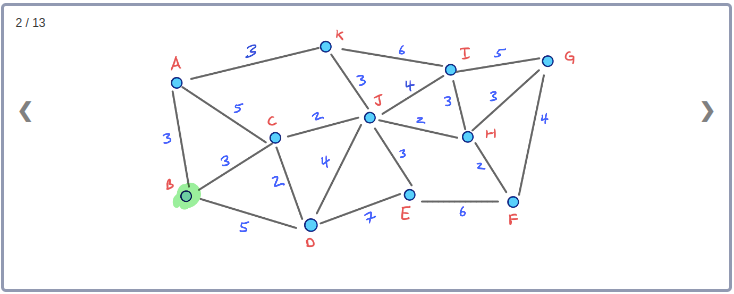
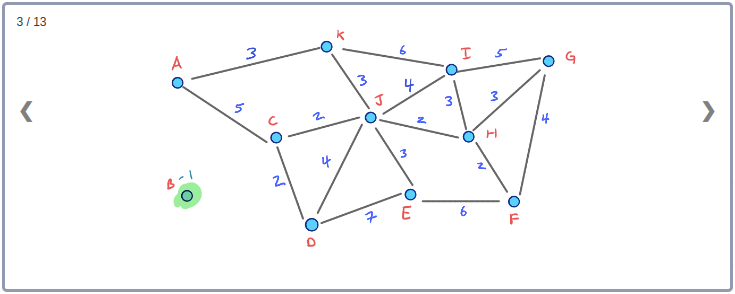
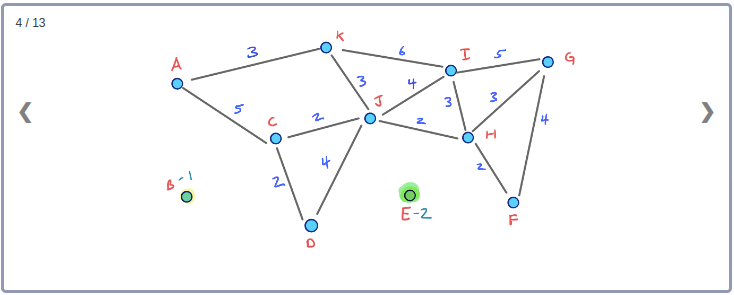
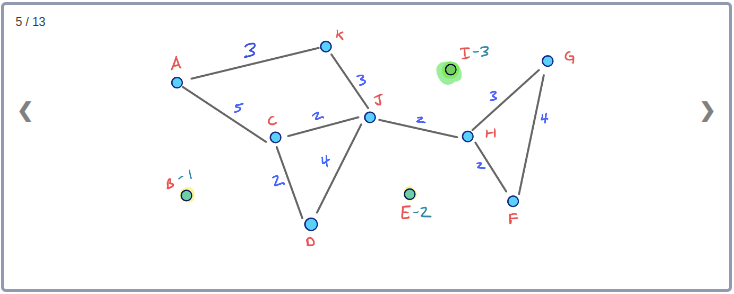
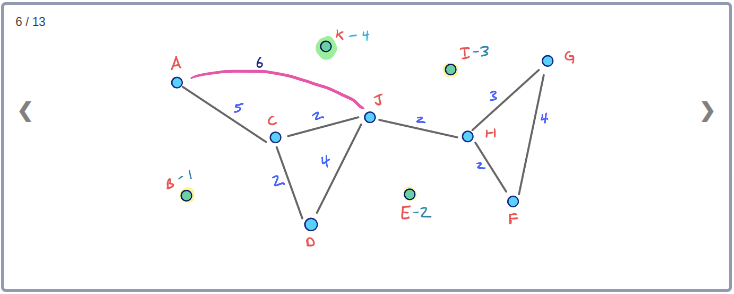
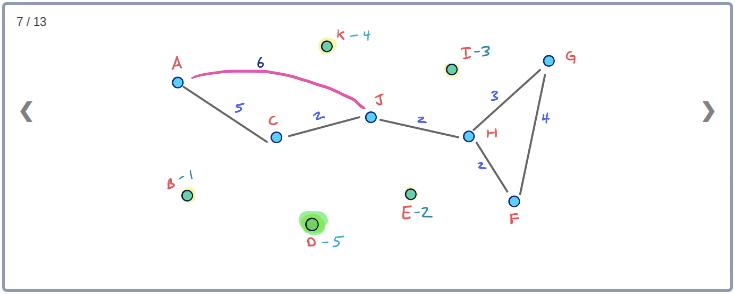
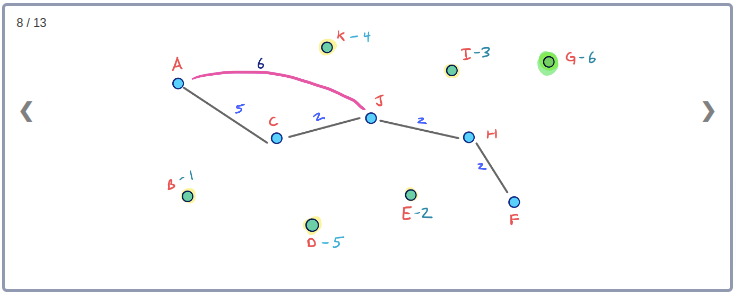
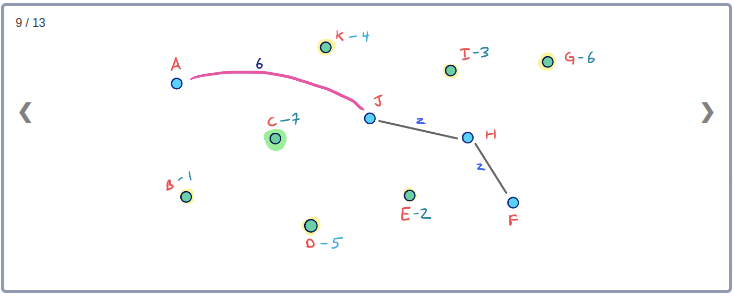
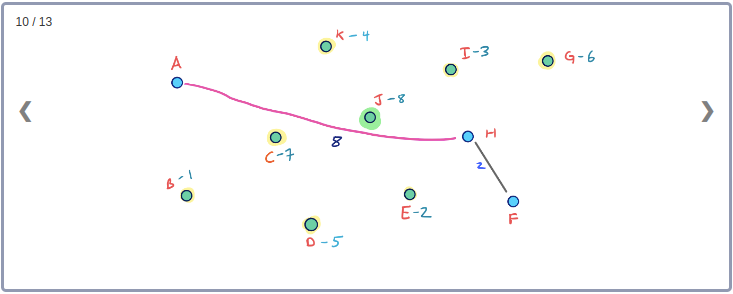
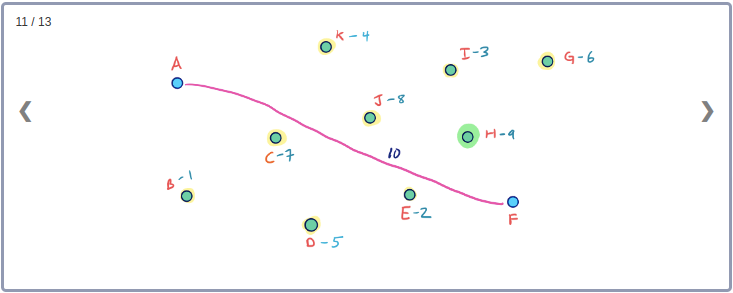
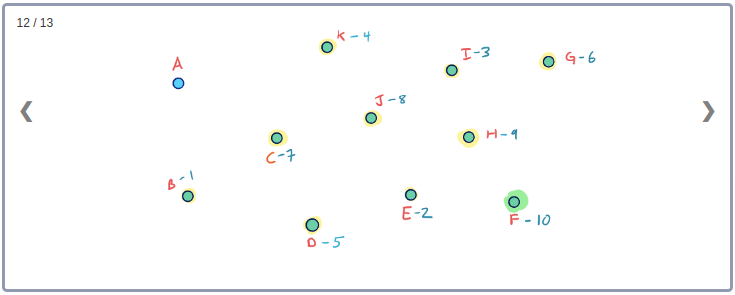
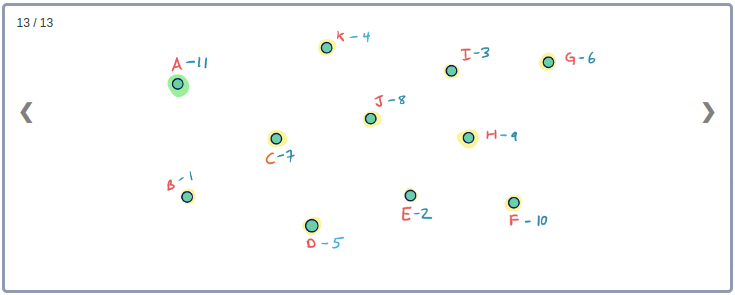
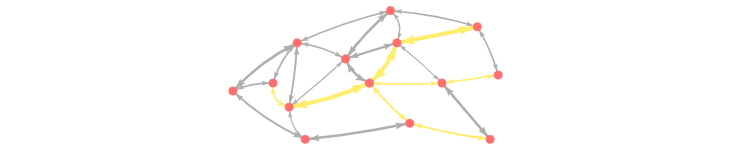
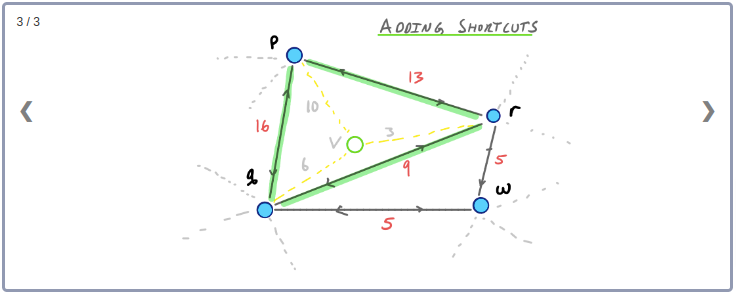
이 Contraction 과정을 통해 아래와 같이 최종적으로 만들어진 G* Overlay 그래프를 시각화 할 수 있다. 이 그래프에는 초기의 그래프인 G와 Contraction과정에서 추가된 3개의 지름길 Edge가 같이 포함된다.

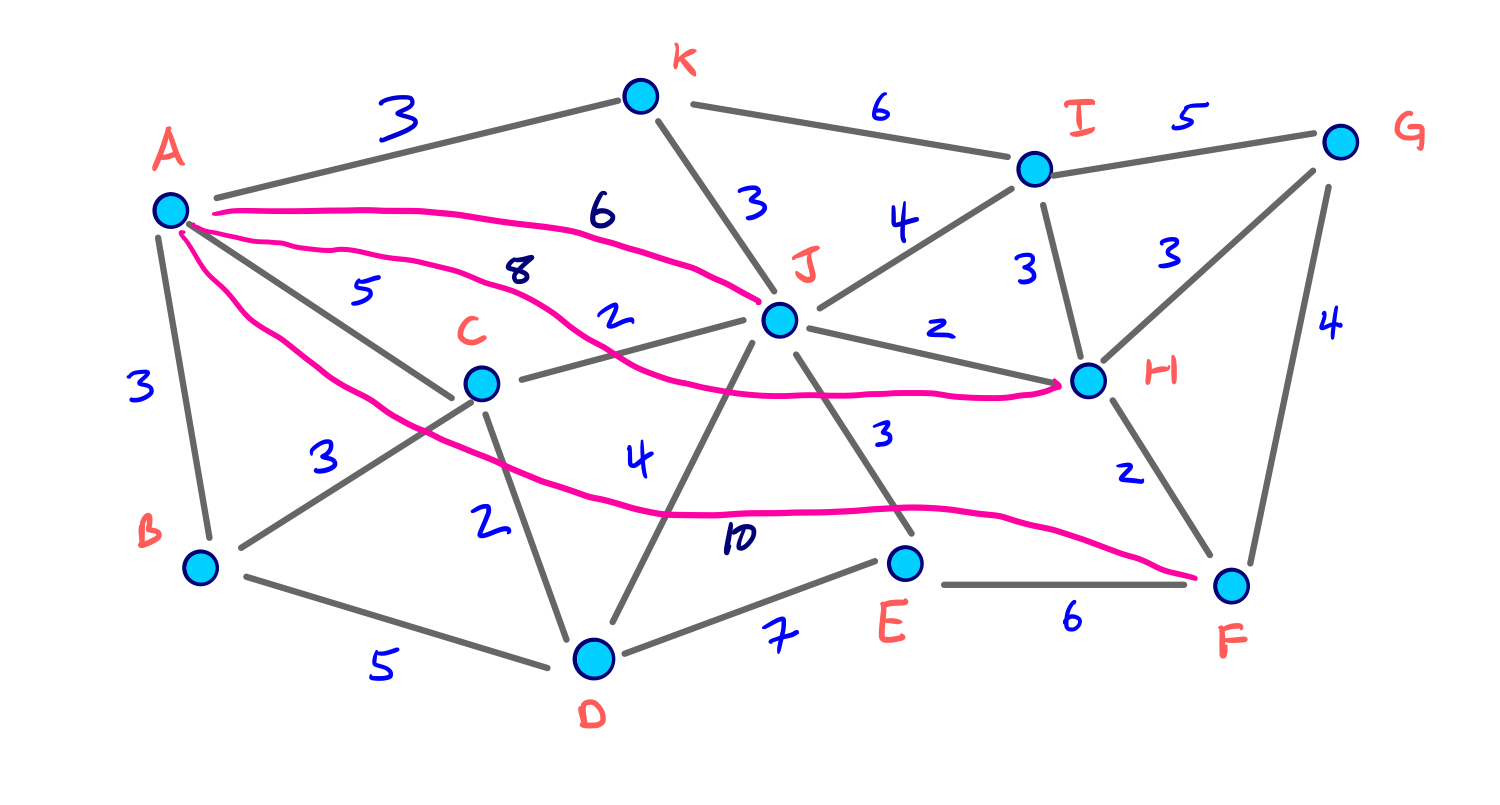
이 그래프에서 지름길 Edge들은 최단거리를 유지하고 있음을 확인할 수 있다. 또한, Node의 Contraction 순서를 바꾼다면 서로 다른 형태의 지름길 Edge들이 만들어질 수 있다. (추후에 다시 다룰 예정)

하지만 당분간은 지금 적용한 Node Ordering이 단지 3개의 지름길 Edge만 추가했으므로 비교적 좋은 Ordering라고 생각하자.

추가할 지름길을 효율적으로 계산하는 방법

앞에서 예로 든 그래프는 눈으로 대충 봐도 Contract될 Node가 이웃하는 두 Node들 사이에서 최단경로인지 쉽게 알아볼 수 있다. 하지만 일반적으로 지름길 Edge를 추가할 때 효율적인 지름길 판별 방법이 필요하다.

지름길 추가(Adding Shortcuts)

복기해보자면, Node v를 Contract하려고 할 때 v로 인입하는 Edge(링크)의 from쪽 Vertex(노드)들의 집합을 U, v로부터 뻗어 나가는 Edge의 to 쪽에 있는 Vertex들의 집합을 W라고 할 때 집합 U에 속해있는 노드 u와 집합 V에 속해있는 노드 v가 있을 경우 경로 <uvw>가 u에서 w로 가는 최단경로일 경우에만 지름길 Edge uw를 추가한다고 했다.

직관적 접근(A straightforward approach)

어떤 지름길이 필요한지 바로 알아 보려면 집합 U에 있는 모든 노드 u에 대해 v를 제외한 상태에서 지엽적(local) 최단경로 탐색을 해보면 된다. 만약 w(u v) + w(v, w) 보다 짧은 거리로 집합 W에 있는 노드 w에 도달할 수 있다면 새로운 최단경로를 찾았으므로(witnessing) 경로 <uvw>는 이제 u에서 w로 가는 최적경로가 아닌 상태가 된다.

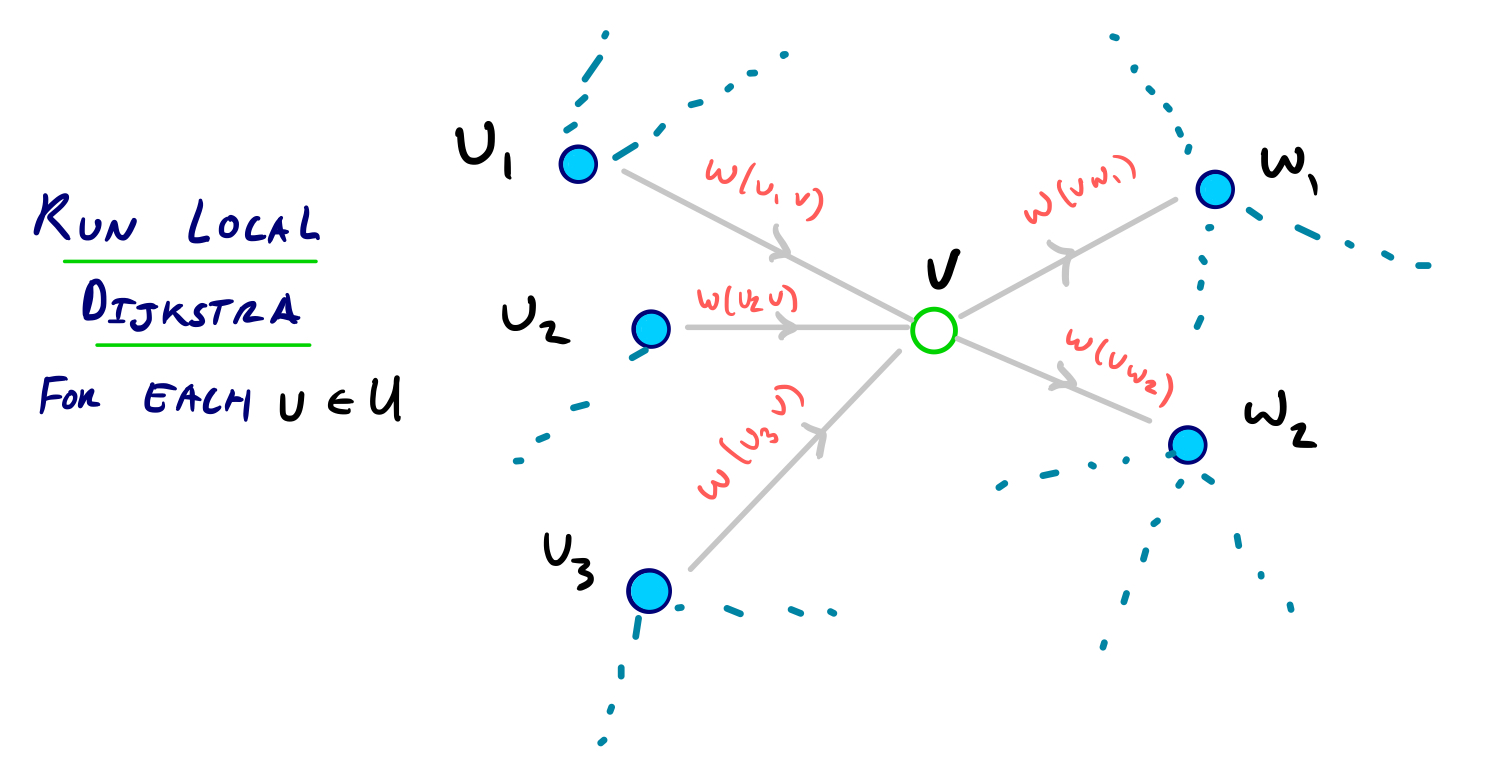
다르게 보면, 경로 <uvw>가 u에서 w로 가는 최단거리이면서 유일한 경로일 경우 v를 제외한 상태의 서브그래프도 고려해야 하므로 local 탐색은 계속 이어나갈 것이다.

따라서 집합 U의 속한 모든 개별 노드 u에 대해 아래의 과정을 수행한다.

1. 집합 W에 속한 모든 노드 w에 대해 v를 거쳐 u에서 w로 가는 경로의 cost인 P_w 를 계산한다. 이 값은 두 Edge 의 합이 된다: w(u, v) + w(v, w)
2. P_max는 집합 W의 모든 노드 w들의 P_w 중에서 최대값을 나타낸다.
3. v를 제외시킨 상태의 그래프에서 u를 시작점으로 하는 표준 Dijkstra 탐색을 수행한다.
4. 탐색과정에서 방문한 Node의 최단거리가 P_max’보다 클 경우 탐색을 종료한다.

그런 다음 Dijkstra 탐색을 통해 얻은 v를 거치지 않으면서 각 w에 이르는 최단거리가 P_w보다 크다면 즉, dist(u, w) > P_w를 만족하면 지름길 Edge인 uw를 추가하고 최단거리(weight)는 Pw’가 되도록 설정 한다. 이 조건을 만족하지 못한다면 지름길 Edge는 추가하지 않는다.

검증(Correctness)

앞에서의 설명은 Dijkstra 탐색으로 방문한(settled) 노드의 최단거리가 P_max’보다 클 경우 탐색을 종료한다고 했다. 그러면 집합 U에 속해 있는 노드 u에 대해 집합 W의 노드 w까지의 최단경로가 존재한다면 이 경로의 길이는 P_w’보다 작으며(P_w’가 v를 지나가는 w’으로 가는 최단경로로 인지하고 있으므로) 결과적으로 P_max’보다 작거나 같다라고 할 수 있다. 따라서, 최단거리가 P_max’보다 커질 경우 탐색을 종료한다는 조건은 노드 u에서 시작되는 local 탐색 과정에서 방문한 모든 w의 최단거리 dist(u, w)가 도출되었음을 유추할 수 있다. 아래 예제를 살펴보자.

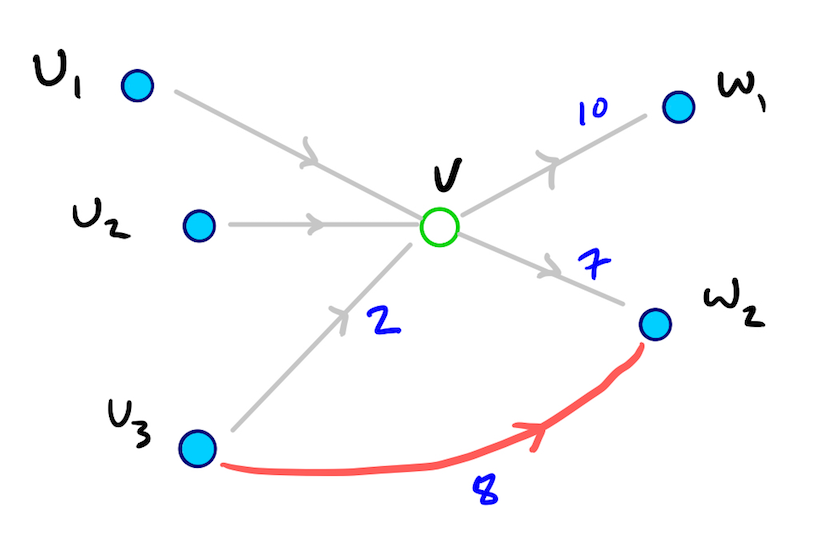
여기서 u3에서 시작하는 local Dijkstra탐색을 수행할 경우 P_max는 12가 된다. 따라서 u3와 w2사이의 최단경로를 나타내는 빨간색 edge는 탐색이 종료되기 전에 갱신(relax)된다. 이 경우 u3와 w2사이 최단거리가 8이되며 v를 지나가는 경로의 거리 9보다 작으므로 지름길 Edge는 추가되지 않게 된다.

이런 local 탐색 비용이 얼마나 높을까?

노드를 contract하기 위한 Local Dijkstra탐색 비용이 높을 수 있다. 예를 들어 P_max가 비교적 큰 값(긴 거리)이라고 하면 최단거리 P_max’보다 긴 거리의 노드까지 방문(settle)해야 하므로 다소 시간이 소요될 수 있다.

일부에서는 local Dijkstra탐색에 heuristic을 적용하는 경우도 있다. 예를 들어, local 탐색에서 방문(settle)하는 노드의 개수를 제한하기도 한다. 종료조건인 최단거리가 P_max’보다 긴 거리의 노드에 도달하기 전에 이 제한치(threshold)에 도달하게 되면 탐색을 종료한다.

이렇게 하면 실질적으로 불필요한 지름길 Edge가 추가될 수도 있다. 이는 최단거리가 아닐 수도 있는 경로<uvw>에서 u와 w사이의 지름길 uw를 추가해버리게 되는 셈이 된다.

그럼에도 지금길 Edge는 최단경로 구조를 유지하기 때문에 중복된 지름길 Edge를 추가한다고 해서 정상적인 탐색을 방해하지는 않는다. 하지만 최종으로 만들어질 덧댄(Overlay) 그래프의 밀도에 영향을 주며 필요 이상으로 생성된 많은 지름길 Edge들로 인해 탐색 시간이 느려질 수 있다.

이런 local Dijkstra탐색에 탐색 공간의 크기를 제한함으로써 전처리에 소요되는 시간을 획기적으로 줄이고 불필요하게 추가된 지름길 Edge들의 갯수가 탐색시간에 많은 영향을 주지 않는다면 정확도가 좀 떨어지는 heuristic을 사용하는 것은 도움이 될 수 있다.

이런 Tradeoff는 실제 구현과정에서 적용해 볼만하다. 그러나 위에서 설명했던 간단한 방법도 Contraction 단계와 Query단계 모두에서 모두 적정한 성능을 발휘했다.

그러나 앞서 말했듯이 필요성이 있는 지름길 Edge는 비록 계속된 추가로 인해 거추장스럽더라도 탐색의 정확도에는 영향을 주지 않는다. 그리고 일반적인 도로네트워크의 평균 노드 차수(노드와 연결된 다른 노드)가 2.5인 점을 감안하면 local 탐색시간은 일정함(constant time)을 예상할 수 있으며 이는 Node의 수와 비례적으로(linear time) 소요시간이 증가함을 의미한다.

변형된 양방향 탐색(Query)

이제 전처리 단계에서 처리했던 것들에 대해 고민해 보자

1. 모든 노드를 중요도에 따라 줄세우기
2. 줄세운 순서에 따라 각 노드를 Contract하기
3. 기존 그래프에 있던 Node와 Edge에 Contraction단계에서 지름길 Edge들을 추가한 덧댄(Overlay) 그래프 G* 생성

이제 출발지 s와 목적지 t 사이에 최단거리를 찾기 위한 그래프 탐색(Query)를 수행해 보자

CH의 탐색은 변형된 양방향 Dijkstra를 이용한다. 그러나 각 탐색 방향별로 그래프 G*의 규모를 축소시킨 서브 그래프를 대상으로 적용한다. 이를 upward그래프와 downward그래프로 부르기로 한다.

앞선 Contraction 예제에서 생성했던 G*그래프를 복기해 보면 적용했던 노드의 순서를 아래 두번쨰 그림에서 확인할 수 있다.

상향(upward) 하향(downward) 그래프

노드의 순서를 고려해서 노드 v가 노드 w보다 나중에 Contract되었다면 v > w (v의 우선순위가 w보다 높음)로 표시한다. 그리고 노드 w보다 이전에 노드 v가 Contract되었다면 v < w로 표시한다.

그러면 상향 그래프와 하향 그래프를 아래와 같의 정의할 수 있다.

상향 그래프(Upward graph) G*_U는 from 노드 v와 to 노드 w로 이루어진 Edge(링크)들로만 구성된다. 이때 v > w 조건을 만족한다.

하향 그래프(Downward graph) G*_D는 from 노드 v와 to 노드 w를 가지는 Edge(링크)들로만 구성된다. 이때 v < w 조건을 만족한다.

모든 노드들은 각자 고유한 순서를 가지므로 모든 Edge는 상향이거나 하향인 그래프에 포함된다.

양방향 탐색공간(Bidirectionl Search Spaces)

오리지널 양방향 탐색은 출발지에서 순방향 탐색을 하고 목적지에서 역방향 탐색을 수행한다. CH에서 노드 s와 t 사이의 경로탐색은 그래프 G*_U의 노드 s에서 순방향 탐색을 하고 그래프 G*_D의 노드 t에서는 역방향 탐색을 진행한다.

그러나 대칭(symmetric) 그래프일 경우 그래프 G*_D에서의 역방향 탐색(링크를 뒤집어서 탐색)은 그래프 G*_U에서 순방향 탐색과 동일하다. 따라서, 그래프 G*_U상에서 출발지와 목적지 노드로부터 동시에 출발하는 표준적인 Dijkstra 탐색을 수행하면 된다.

앞 선 예제를 활용해서 출발지노드가 B이고 목적지 노드가 G라고 해보자. 그러면 그래프 G*_U에서 양방향별 탐색 공간은 아래와 같이 형성된다.

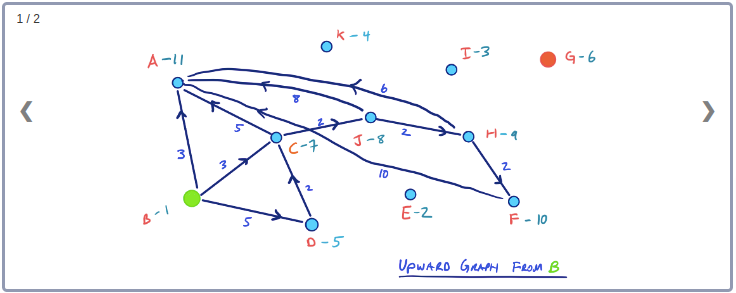
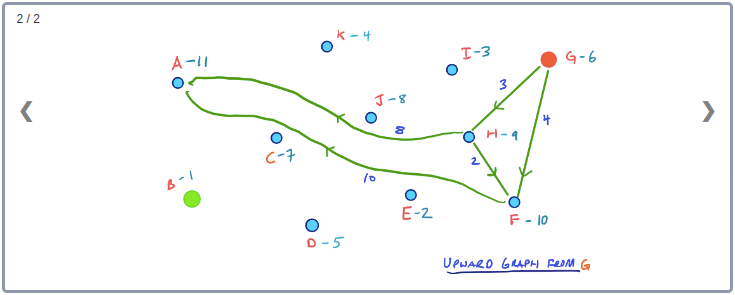
그래프 G*에 속한 모든 Edge는 그래프 G*_U 또는 그래프 G*_D에 속하게 된다고 하더라도 그래프 G*_U의 모든 Edge가 주어진 시작 Node에서부터 만들어지는 탐색공간에 포함되지 않을 수도 있다.

위 예제에서 Edge ED의 경우 E가 D보다 먼저 Contract되므로 그래프 G*_U에 존재하지만 출발지 B와 G에서 E까지 가는 경로가 존재하지 않아 Edge ED는 고려할 필요가 없다.

이들 두 개의 상향 그래프를 대상으로 완전한 Dijkstra 탐색을 수행한다. 이는 양방향 서브그래프상의 모든 노드들은 반드시 방문(settled)됨을 의미한다. 그리고 양방향 탐색은 특성상 방문된 노드의 수와 relax된 Edge의 갯수는 그래프 G* 전체 탐색(한 방향)과 비교했을 때 훨씬 적을 것이라는 것은 명확하다.

더욱이 모든 노드를 완전한 형태로 줄세웠기 때문에 두 탐색공간은 DAG(Directed Acyclic Graph)그래프로 나타낼 수 있으며 형태상(topologically)으로는 정렬된 상태가 된다. 두 탐색과정을 그림으로 표현해보면 Contraction 순서의 계층적 특성을 명확히 알 수 있다.

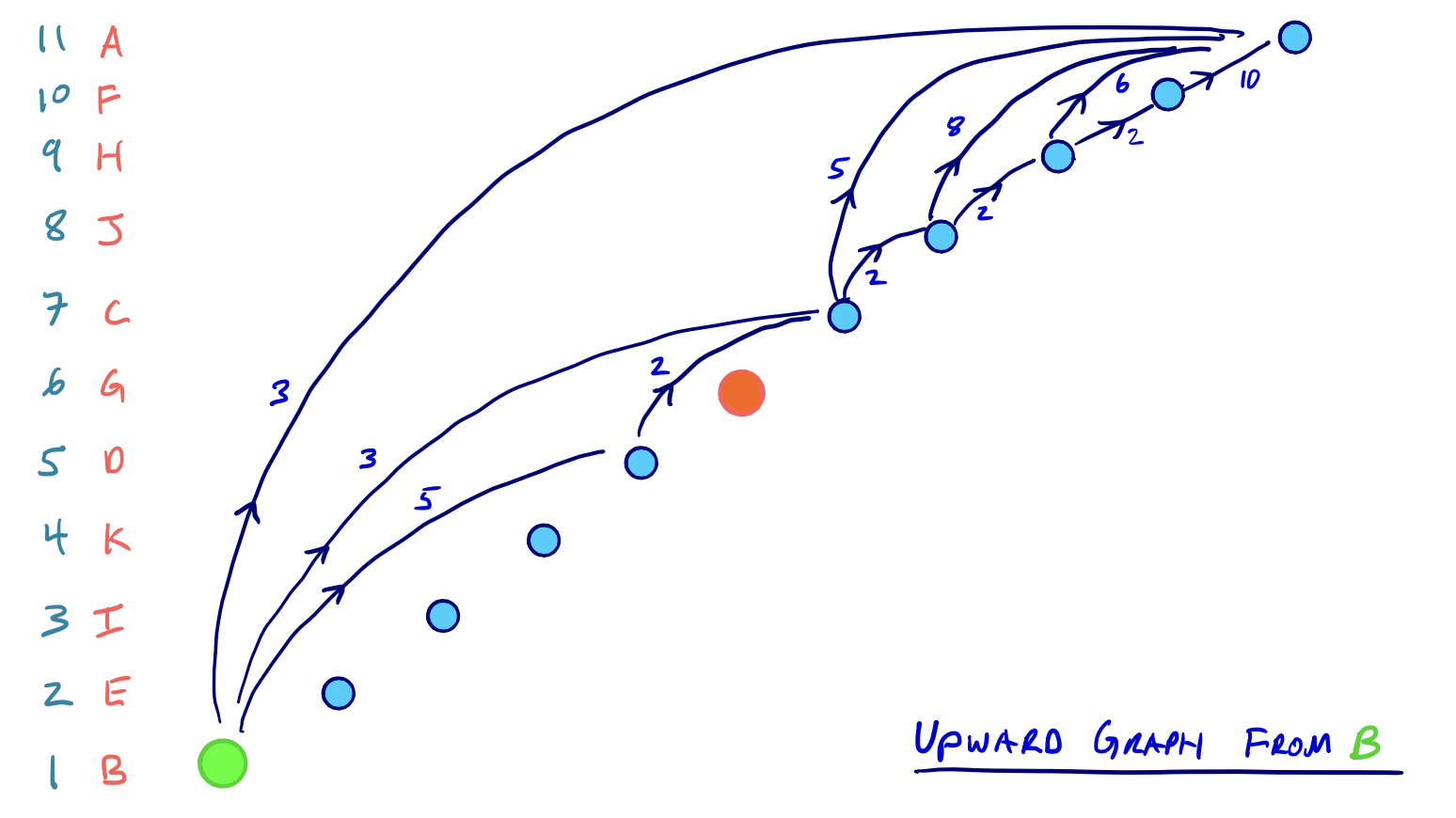
최단경로 거리 도출

어떤 경우에라도 그래프 G*_U의 출발지와 목적지에서 양방향 Dijkstra 탐색을 수행하면 두 탐색공간에서 공통으로 방문된 노드들이 존재하며 이들 노드 집합을 L로 표현한다.

위의 예제를 가지고 얘기를 이어가자면 집합 L의 노드 중 최단거리를 빨간색으로 칠한 노드들을 볼 수 있다.

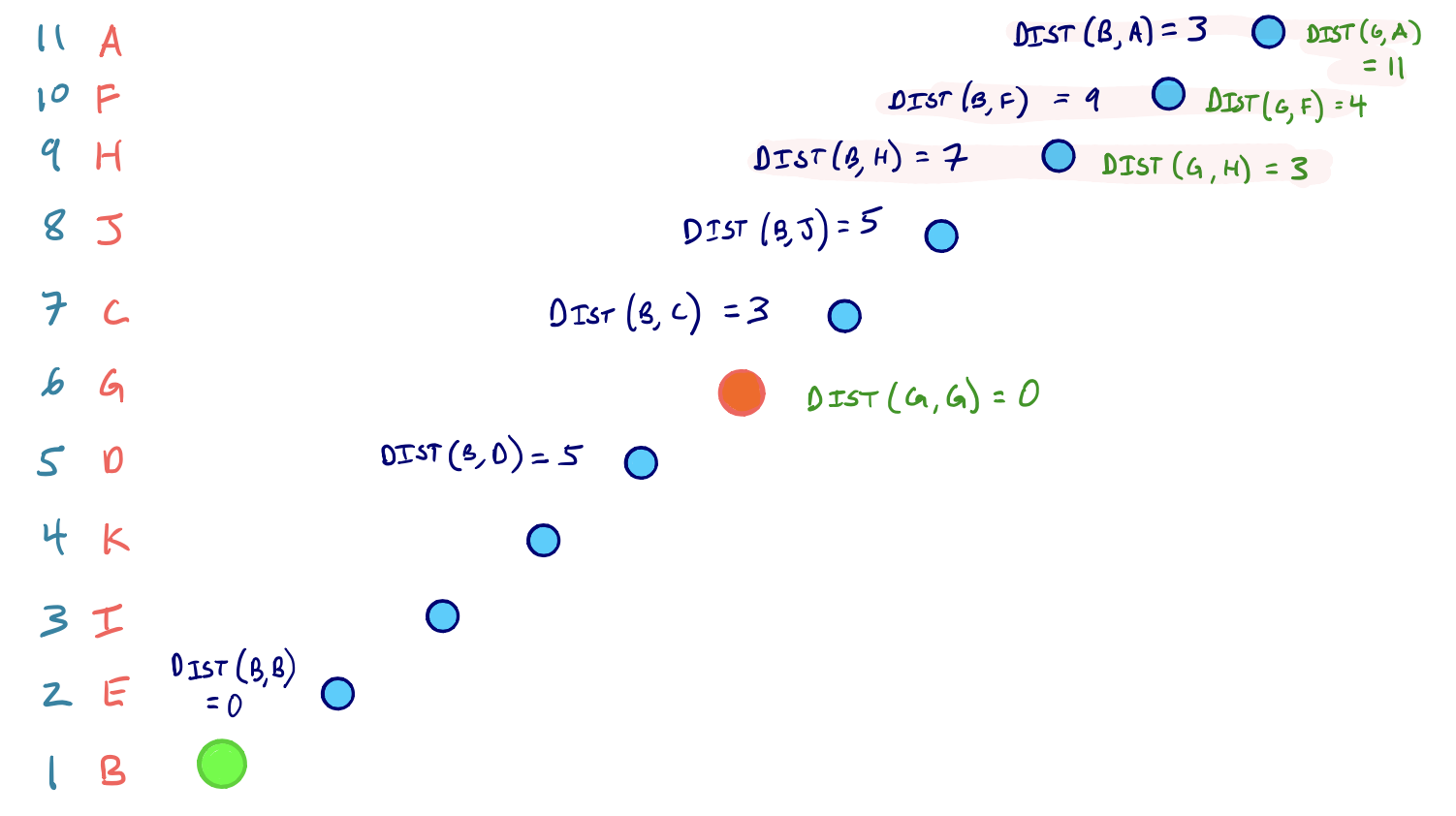
집합 L에 속한 모드 노드 v에 대해 노드 v까지의 최단거리를 합산했다(s로부터의 거리와 t로부터의 거리). 최단경로의 거리는 집합 L에 속한 모든 노드 v에서 거리합(정방향/역방향)이 최소인 값이 된다.

다시 말하면 아래와 같이 표현할 수 있다.

dist(s, t) = min{ dist(s, v) + dist(v, t) } over v in L

따라서, 위 그림을 보면 출발지 노드 B와 목적지 노드 G에 대해 3개의 노드 즉, H, F, A가 방문(settled)되었다. 그리고 노드 H가 dist(B, H) + dist(G, H) = 10 이 되므로 이들 3개의 Node 중에 최소값을 가진다.

이는 B와 G사이에 최단경로의 거리는 10이 되고 H를 통과함을 의미한다. 아래 G*그래프에서 이를 확인할 수 있다.

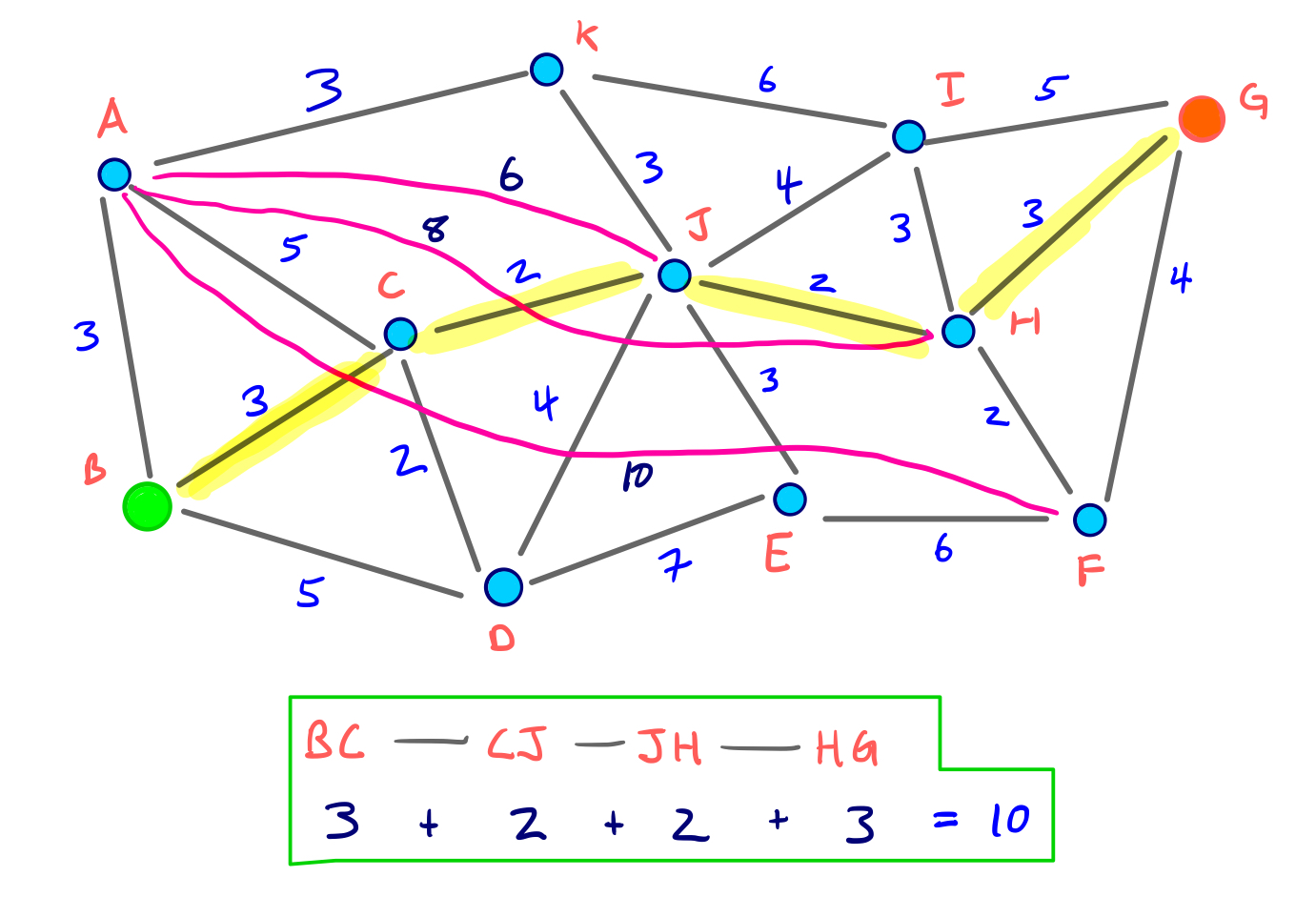
양방향 Dijkstra 탐색은 정확한 경로를 산출하며 탐색하는 동안 16개의 Edge(링크)만 relax한 셈이 된다. 이는 원래 그래프일 경우 40개의 Edge를 relax해다 하는 것과 비교하면 많이 줄어든 것임을 확인할 수 있다.

위의 예와 같이 규모가 작은 그래프를 대상으로 할 경우 속도향상이 눈에 띄지 않지만 실제 도로네트워크에 적용하면 탐색공간을 엄청나게 줄일 수 있다.

지름길 경로 복원

최단경로의 거리를 도출할수 있지만 여기에 더해 지름길 경로에 포함된 실제 링크들도 복원시켜야 한다. Contraction과정에서 지름길 Edge를 추가할 때 이 과정을 처리할 수 있다. Node v를 Contraction하는 과정에서 Node u에서 w로 가는 지름길 Edge를 추가할 때 v를 가리키는 지름길 Pointer도 같이 저장한다.

양 방향의 그래프 G*_U에서 최단경로를 복원할 때 중요도가 가장 높은 Node부터 시작한다. 일반 Dijkstra Algorithm에서 이전 링크를 찾아가는 방식처럼 부모 Edge를 역으로 추적해 나가면 된다. 부모 Edge가 지름길 Pointer를 포함하고 있다면 부모 Edge를 지름길 Edge로 치환하며 전체 경로를 복원할 때까지 재귀적으로 이 과정을 수행해 나간다.

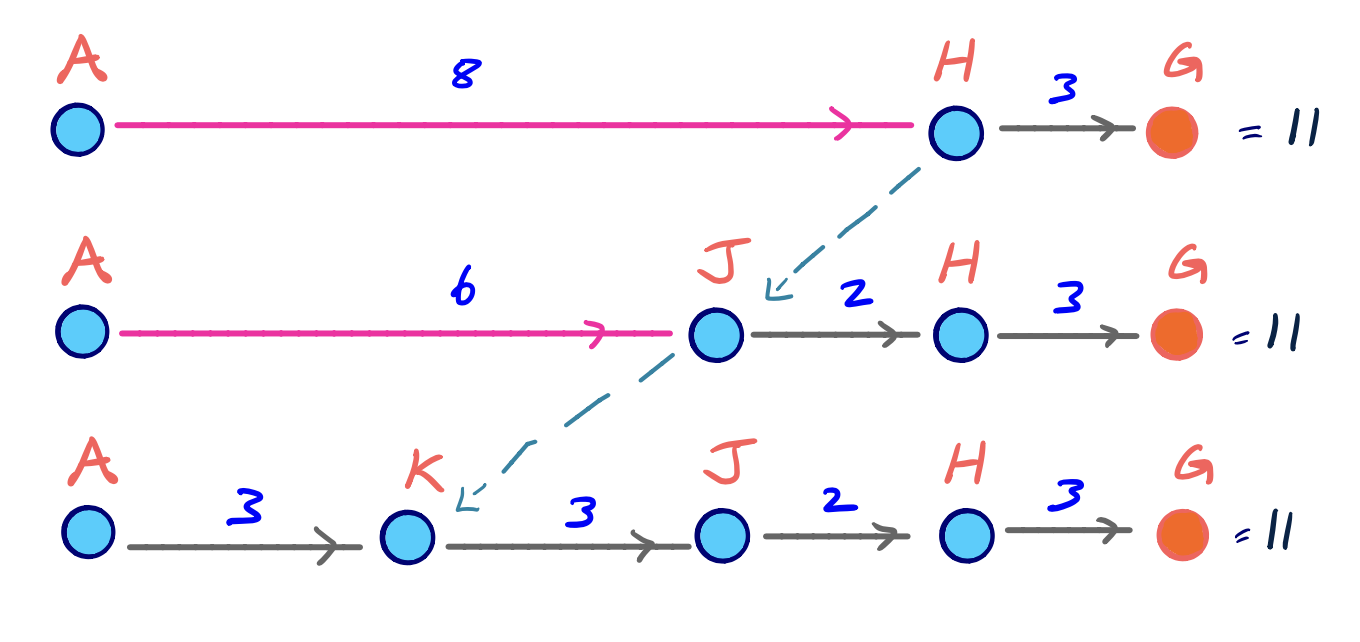
위의 탐색 예제에서는 지름길 경로가 포함된 형태로 만들어지지 않았다. 하지만 노드 A에서 G로 가는 최단경로를 탐색한다고 생각해보면 지름길 경로 AH가 반드시 포함될 것이다. 여기서 Contraction이 이루어진 순서상으로 보면 노드 A의 우선순위가 가장 높기 떄문에 지름길 경로의 복원과정을 아래와 같이 시각화 할 수 있다.

탐색 검증(Query Correctness)

임의의 Contraction순서로 만들어진 그래프 G*상에서 앞에서 설명했던 탐색(Query) Algorithm이 정확하게 동작하는지를 설명하려고 한다. 나아가 그래프 G*에서의 최단경로가 원본 그래프인 G에서도 최단경로가 되는지도 같이 살펴보도록 한다.

표기법 설명

앞에서 설명할 때 활용하긴 했지만 다시 복기하자면

• 집합 V에 속한 모든 노드 v 에 대해 노드 순서는 O = {v₁, …, v_n} 로 표기
• 원본 그래프 G를 G₀로 표기하고 그래프 G_i-1의 노드 v_i를 Contraction함으로써 생성된 서브 그래프를 G_i라고 표기
• 이제 G_i는 v_i , 그리고 v_i와 인접한 Edge들이 제외된 상태임. 그러나 v_i가 Contract되면서 새로 추가된 지름길 Edge들은 포함하고 있음. 따라서 G_i는 n-i 개의 노드로 구성됨.
• 그래프 G_i상의 두 노드 u, v 사이의 최단경로는 dist_i(u, v)로 표기 함
• 덧댄(Overlay) 그래프 G*는 그래프 G의 모든 노드와 Edge에 더해 그래프 {G₁, … G_n-1}에서 추가된 모든 지름길 Edge들도 포함하고 있음

보조명제 1: 모든 노드를 대상으로 Contraction하더라도 최단경로는 유지된다.

이는 두 노드상의 최단경로는 Contraction 전과 후가 동일하다는 것을 의미한다.

표현하자면:

그래프 G_i의 모든 노드 s와 t에 대해 dist_i(s, t) = dist_i-1(s, t)을 만족한다. 이때 i 는 [1, n] 사이의 값을 나타냄

그래프 G_i의 노드 s에서 t까지의 최단경로 P가 있다면 v_i가 Contraction 된 후 P는 지름길 Edge를 포함할 수도 있고 그렇지 않을 수도 있다. 만약 지름길 Edge가 포함되지 않는다면 P는 그래프 G_i-1에도 반드시 존재한다. 만약 Contraction과정에서 P가 지름길 Edge를 포함할 경우 u와 w가 v_i의 이웃노드이고 지름길 Edge를 uw라고 가정해보자. 그러면 그래프 G_i-1에서는 경로 중 cost가 uw와 동일한 경로 <uv_iw> 가 존재할 것이다. 왜냐하면 v_i를 contraction한 후 지름길(uw)을 추가했기 때문에 당연한 얘기가 된다. 따라서 dist_i-1(s, t) <= dist_i(s, t)가 된다.(???, = 일 것으로 추정)

비슷한 방법으로 이제 그래프 G_i-1에서 노드 s부터 t까지의 최단경로가 있다고 생각해보자. P가 v_i(다음 round에서 Contraction될 노드)를 통과하는 Edge를 가질 수도 있고 아닐 수도 있다. 만약 v_i를 통과하지 않는다면 최단경로 P는 G_i에서 존재하는 것과 같이 그래프 G_i-1에서도 동일하게 존재하고 있을 것이다. 만약 P가 v_i를 통과하는 Edge를 포함한다면 그래프 G_i에서는 동일한 weight(cost)를 갖는 지름길 Edge가 추가될 것이다. 따라서 dist_i(s, t) <= dist_I-1(s, t)가 성립한다. (???, = 일 것으로 추정)

따라서, dist_i(s, t) = dist_i-1(s, t)가 성립한다.

이 결과는 대체로 명료하지만 시각적인 예제가 필요하다면 초기 contraction 예제를 생각해보면 된다.

탐색(Query)는 정확하다(Query is Correct)

아래의 식을 증명하기 위해 명제 1을 활용한다.

dist(s, t) = min{ dist(s, v) + dist(v, t) } over all v in L

여기서 L을 그래프 G*_U의 Node s와 t에서 시작하는 양방향 탐색에서 모두 방문한(settled) 노드 집합이라고 하자. 이제 그래프 G에서 노드 s부터 t까지 최단경로를 생각해보자. 여기서 경로 P상에 있는 노드 중 우선순위가 가장 높은 노드(맨 나중에 contract된 노드)를 vertex m 이라 정의한다.

추후에 보강 예정…

노드 순서 선정

노드가 contract되는 순서와 상관없이 탐색은 정상적으로 동작한다. 그러나 노드 줄세우기를 어떻게 하느냐에 따라 탐색 성능에는 많은 영향을 줄 수 있다. 지름길 Edge가 그래프 G*에 추가될지 여부는 노드가 Contraction되는 순서에 영향을 받는다. 앞서 언급되긴 했지만 지름길 Edge가 너무 많아지면 그래프 G*의 밀집도가 높아지고 이로 인에 탐색 성능이 떨어지는 결과를 초래한다.

따라서 CH에서의 최대 관심사는 전처리(Preprocessing) 단계에서 어떻게 노드를 줄세울 것인가가 된다. 이상적인 노드 줄세우기는 쉽지 않은 것으로 알려져 있다. CH와 관련된 많은 연구와 개발 과정에서 어떻게 하면 노드 줄세우기 를 잘 할 수 있을지를 다루고 있다. 그 중 아래와 같은 방법은 실제 적용했을 때 높은 성능을 보여 준다.

노드 줄세우기 전략

일반적으로 생각해 볼 수 있는 방법은 모든 노드마다 Contract 수행과 관련된 일종의 Cost를 부여하고 Cost가 가장 적은 것부터 가장 높은 것까지 줄을 세우는 것이다. 초기에 얘기했던 것처럼 Cost를 중요도를 나타내는 척도로 생각해 볼 수 있다.

이 Cost를 산정하기 할 때 주로 적용하는 기능으로 각 노드를 대상으로 Contraction을 시뮬레이션 해보는 방법이 있다. Contraction과정에서 특정 노드와 인접한 모든 Edge들을 제거한다고 했을 때 노드에 연결된 Edge들의 갯수 차이를 활용한다. 즉 초기의 Edge 상태에서 제거된 Edge 개수와 새로 추가된 지름길 Edge 갯수의 차이를 이용한다.

앞에서 봤던 그래프를 다시 가져오면

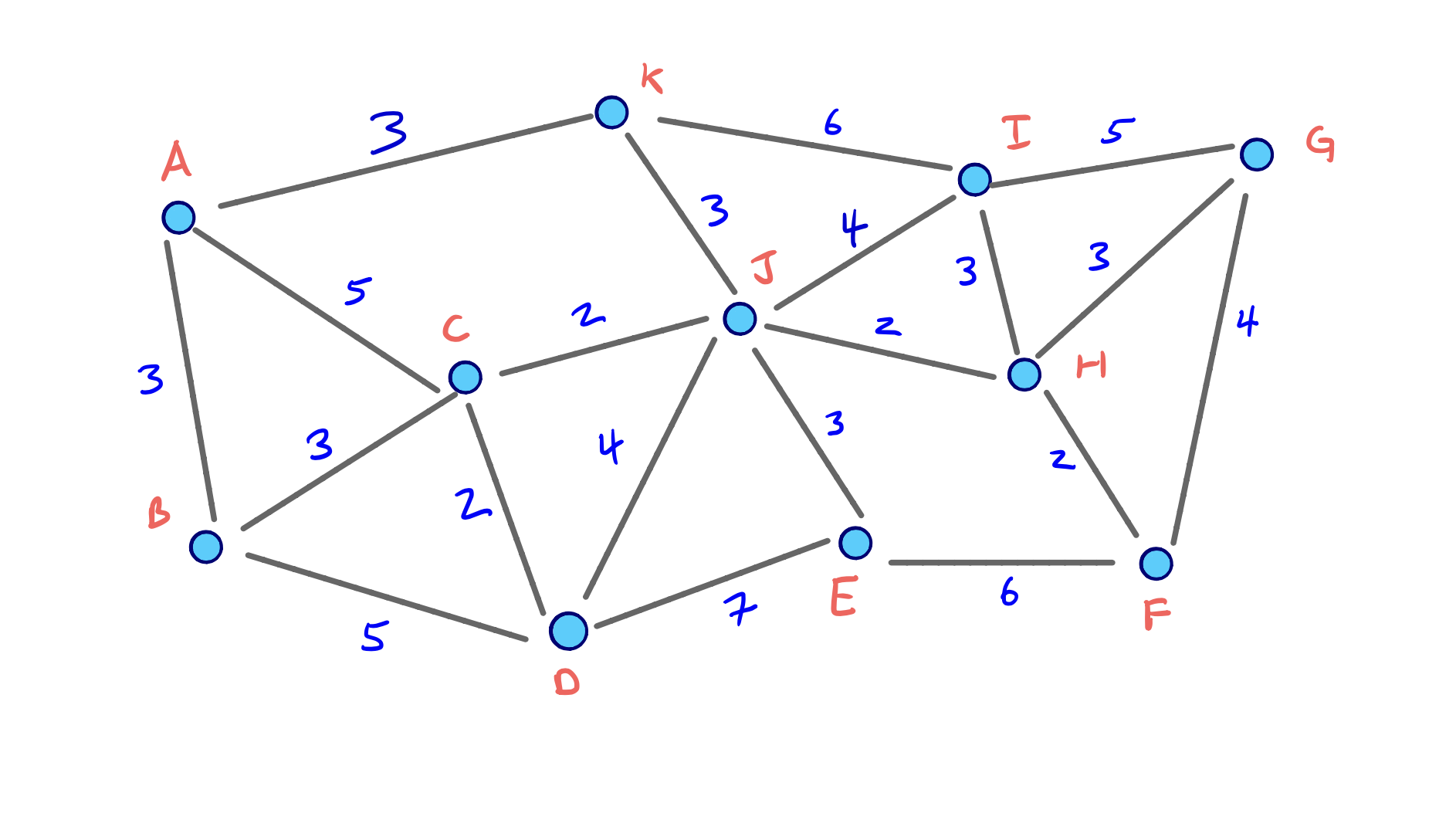
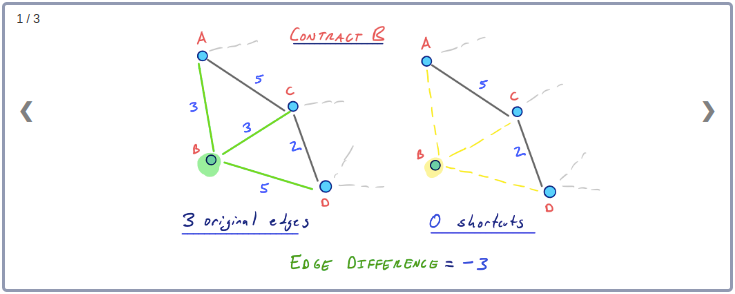
처음에 임의로 정의한 노드 순서를 이용할 경우 단지 3개의 지름길 Edge만이 최종 추가되었다. 최초로 노드 B가 Contract되었지만 이 과정에서는 지름길 Edge는 추가되지 않았다. 다시말해 노드 B의 Edge Difference는 -3이 된다.

그러나 노드 J를 먼저 Contract 한다면 어떻게 될까? B대신 노드 J를 선택하면 어떻게 되는지 비교해 보자.

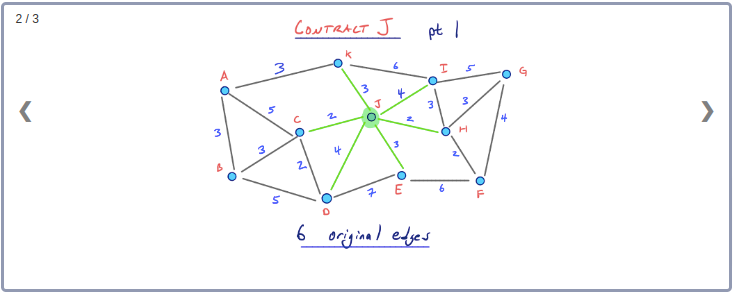
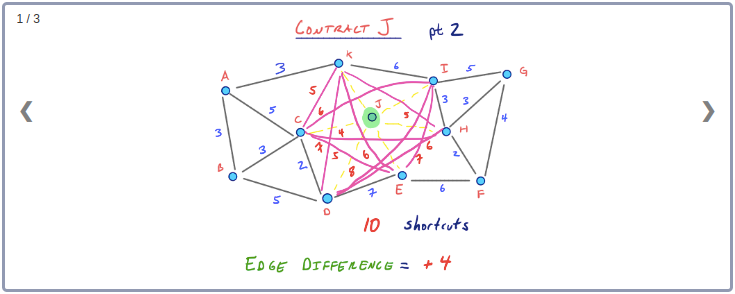
노드 J는 B보다 훨씬 큰 Edge Difference를 보여준다. 따라서 초반부에 J를 contract한다는 것은 좋아보이지 않는다. 노드 J의 경우는 이웃 노드들과 낮은 Cost의 Edge로 연결되는 중심부에 있다. 이때 인접하는 Edge들은 노드 B와 G사이의 최단경로에서 처럼 먼거리를 여행할 때 경로 중반부에 주로 이용하는 고속도로와 같은 도로에 해당한다. 따라서 J와 같은 노드는 중요도가 높은 노드이며 최고의 탐색성능을 기대한다면 초기에 contract 해서는 안된다.

순서계산과 Node Contraction

노드순서를 결정하고 이 정해진 순서대로 Contraction을 수행하는 초기 방법으로 Cost Function에 기반하여 일종의 Priority Queue를 적용해 볼 수 있다. 이 경우 Priority는 각 노드별 Edge Difference가 된다.

따라서, 먼저 Priority Queue를 로딩하려면 각 노드가 Contraction될 때를 시뮬레이션해서 Edge Difference를 계산한다. 앞에서 다뤘던 지름길 Edge 계산 방법을 활용해서 각 노드마다 일련 계산 작업을 수행한다. 이 단계의 작업은 노드 개수에 비례한 작업시간이 소요된다.

그러나 노드 Contraction작업 시작 이후에는 다른 노드들의 Edge Difference에도 영향을 줄 수 있다는 점을 고려해야 한다. 만약 Edge개수 차이를 기준으로 노드 줄세우기를 엄격하게 적용할 경우 Contraction 수행 후에 그래프에 남아 있는 모든 노드를 대상으로 Edge Difference 재계산 해야 할 수 있다. 물론 이렇게 하면 엄청난 시간이 소요될 것이며 현실적으로 수행이 불가능하다. 대신 한 연구에서 제시된 lazy update 휴리스틱 방법을 활용해 볼 수 있다.

Lazy Updating

이 휴리스틱 방법을 활용하기 전에 초기 노드 줄세우기를 이미 끝내놨다고 생각해보자. 이제 Priority Queue에서 가장 낮은 순위의 노드를 꺼내 순서대로 Contraction하는 과정에 들어간다.

차순으로 낮은 순위의 Node를 Contraction하기 전에 이 노드의 Edge Difference를 계산한다. 계산된 값이 여전히 Priority Queue 상의 최소값이면 Contraction을 실제 수행하고 만약 계산된 Edge Difference가 최소값이 아니면 이 노드의 Cost를 갱신하고 Priority Queue를 재정렬한다. 그런 다음 최소 노드를 체크하며 이 과정을 이어 나간다. 이 Lazy Updating 방법을 적용할 경우 향상된 Contraction 순서로 인해 탐색시간 개선으로 이어진다는 연구가 있다.

Priority Queue의 Cost 값을 갱신하기 위한 또 다른 휴리스틱 방법으로 가장 최근에 Contract된 노드와 이웃하는노드의 Edge Difference만을 계산해보는 방법이다. 이후 이어지는 과정에서 lazy update가 과도하게 발생할 경우 전체적으로 남아있는 모든 노드들에 대한 Edge Difference를 재계산해야 할 수도 있다.

그 외의 Cost Function

Contraction에 드는 비용 결정에 활용되는 또 다른 요소를 고려해 볼 수 있다. 예를 들어, 노드를 Contraction할 때 균일성(uniformity)과 같은 아이디어를 중요하게 고려해 볼 수 있다. 이는 Contraction 진행 순서 관점에서 노드의 위치에 변화를 주는 것을 의미한다.

개념적으로 그래프상에서 좁은 지역에 포함되어 있는 모든 노드들을 연속적으로 Contraction하고 싶지는 않을 것이다. 왜냐하면 불필요한 지름길 Edge들이 너무 많이 포함될 위험이 있기 때문이다. 초기 예제에서 비교적 좋은 노드 순서를 부여했었다. 이는 각 Contraction 단계에서 그래프상 서로 다른 영역에서의 노드들이 Contraction되었기 때문이다.

따라서 추가적으로 고려해 볼만한 점은 각 노드의 이웃 노드 중 Contract된 이웃 노드(contracted neighbors) 갯수를 따져보는 것이다. 이는 원본 그래프에서 이미 Contract된 노드들의 갯수를 카운팅하는 것이다. Cost를 결정하는 과정에서 Contracted Neighbors와 Edge Difference와 같이 여러 고려 요소가 있을 때 이들을 조합하는(선형결합) 방법을 적용한다.

노드 줄세우기에 사용되는 개선된 휴리스틱

CH관련 논문 원문에서 노드 순서를 결정할 때 더욱 정교한 항법들을 사용하고 있지만 이 글에서는 다루지 않는다. 좋은 성능의 노드 줄세우기는 Edge difference와 Contracted neighbors를 모두 조합한 형태로 활용한다. 노드 줄세우기가 잘 되어 있으면 탐색시간을 줄일 수 있지만 전처리 단계에서 더 많은 비용을 지불하게 되므로 이 둘의 관계에는 Tradeoff 가 존재한다.

그러나 요약해보자면 Lazy Update 휴리스틱에서 소개한 두 개의 개념은 CH를 적용해보기에 좋은 기반을 제공한다.